INTERPOLAZIONE POLINOMIALE

                  Si consideri l' insieme di coppie

                 ( x1, y1)   ( x2, y2)   ( x3, y3)  ...  ( xn, yn)

                Si tratta di trovare un polinomio, di grado prefissato, che passi il più vicino 

                possibile a tutti quei punti.

                Risolveremo il problema senza ricorrere direttamente al calcolo differenziale,

                ma estendendo ad Rn proprietà del tutto intuitive nel piano o nello spazio.

               Si tratta di un modo di procedere analogico, che si giustifica per la sua 

               immediatezza e per la sua efficacia euristica; in appendice verrà comunque 

              riportata la dimostrazione di quelle proprietà.

             Siano                   X=(x1,x2,x3... xn)

                                         Y=(y1,y2,y3... yn)

           Sia E un insieme di Rn . Cerchiamo un vettore Y°=(y1°,y2°,y3°...yn°) appartenente

           a E il più vicino possibile a Y. 

           E qui sarà un sottospazio e, poiché faremo i disegni nel piano, lo raffigureremo 

           come una retta per l' origine. E' opportuno forse rammentare che questo piano

           rappresenta  Rn , non il piano su cui giacciono i punti ( xi, yi).

           Y° è dato dal piede della perpendicolare calata da Y sul sottospazio E

           La condizione di minima distanza si tradurrà quindi in una condizione di 

          perpendicolarità, ovvero di prodotto interno nullo fra opportuni vettori.

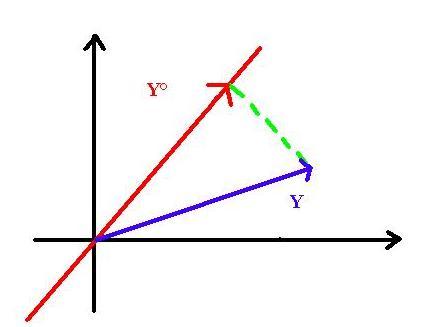
                  Deve essere           ( Y-Y°) * V=0  per ogni generatore V di E

            (Per n=2 E è proprio la retta rossa e V e un qualsiasi suo vettore)

              Consideriamo anzitutto l' interpolazione lineare.In tal caso E è generato da X

              e da U=(1,1,1...1), dovendo essere  Y°=mX+qU                          

               Per semplicità supponiamo q=0 ( è come chiedere che E sia generato dal solo X)

             Allora la condizione di perpendicolarità  diventa        

                                                    X*Y=mX*X 

               e quindi 

                                                    m=X*Y/|| X ||2

              Ora estendiamo le considerazioni precedenti a polinomi di grado r.

              La generica componente di Y0 è del tipo:        

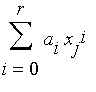
               Poniamo  X[i] =(x1i,x2i,x3i... xni). 

               Allora lo spazio E dovrà essere quello generato da

                                                          X[0] , X[1] , X[2] ... X[r] 

               (nel caso lineare c' erano solo i primi due vettori, indicati con X e U )

               Ora Y-Y° deve essere perpendicolare a ciascuno dei generatori; si ottiene 

               così un    sistema di r+1 equazioni in altrettante incognite, che fornisce 

                i coefficienti   del polinomio approssimante:

                                                                 ( Y-Y°) * X[i]=0

              Analiticamente   ( i=0,1,2...r) :

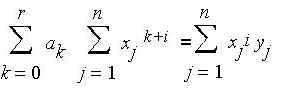
              Si può risolvere il sistema con Excel

              ESERCIZIO  Qual è il polinomio interpolatore di grado nullo?

              ESERCIZIO    Prova che  y-yb=(X*Y/|| X ||2)(x-xb) è la retta interpolatrice:

                                      (xb,yb) è il baricentro dei dati.

               ESERCIZIO Verifica che il metodo esposto, quando Y appartiene a E, fornisce 

                                   Y stesso. (Ne daremo una dimostrazione formale in appendice; 

                                    qui, per   coerenza con l' impostazione intuitiva del discorso, basta 

                                    convincersene geometricamente, visualizzando E come retta o 

                                     piano, oppure,  numericamente, usando il programma in Excel

               PROBLEMA   Esamina cosa succede se si scambiano i ruoli di X e Y.

                Rimane ora da esaminare il grado di approssimazione, definendo un indice che

                misuri quanto  la curva teorica si scosta da quella empirica;il che, nel caso 

                lineare, significa misurare  il grado di allineamento dei dati

                                                                                                         (continua)