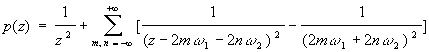 con n m ¹ 0
con n m ¹ 0La funzione p di Weierstrass
di Massimo Fantin
La funzione p di Weierstrass è una funzione di variabile complessa doppiamente periodica con un polo di ordine due nell'origine ed è definita da :
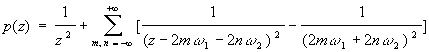 con n m ¹ 0
con n m ¹ 0
w
1 , w 2 rappresentano i semiperiodi.Lo sviluppo di p(z) è dato da
![]()
dove
c2=g2 /20, c3=g3 /28 e per k>3![]()
i coefficienti g1,g2 sono detti "invarianti" e individuano la funzione allo stesso modo dei "semiperiodi".
Oltre alla funzione p(z) studiamo al sua derivata p'(z) il cui sviluppo sarà:
p'(z) = z -3 + 2c2 z + 4 c3 z3 + 6 c4 z 5 + 8 c5 z7+ ….+(2k - 2) ck z 2k - 3 +….
La funzione di p di Weierstrass viene detta funzione ellittica perché permette di parametrizzare le curve ellittiche ( cubiche di equazione y2 = 4 x3- g2x - g3 , dove i coefficienti g sono gli stessi invarianti .
La parametrizzazione avviene osservando dagli sviluppi scritti sopra che p'(z)= 4 p(z)3-g2 p(z)-g3 pertanto la parametrizzazione viene fatta ponendo: x = p(z), y=p'(z)
Studiamo la funzione p(z) nel caso particolare in cui g2=4 e g3=0. Questa permette di parametrizzare la curva ellittica y2=4x3-x
Uso del programma di simulazione
Il programma di simulazione permette di visualizzare sia la funzione p che la sua derivata mediante due rappresentazioni a due colori per ciascuna funzione, una per la parte reale e una per la parte immaginaria. Inoltre è possibile vedere la rappresentazione della p ( grafico blu) e della p' (grafico verse) lungo una sezione del dominio, (corda orizzontale blu nel rettangolo al centro, spostabile con il mouse), inoltre, contemporaneamente compare ( grafico nero) la rappresentazione parametrica della curva ellittica corrispondente a quella data sezione. Si osserva che la curva ellittica reale y2=4x3-x, costituita da due parti, una illimitata e l'altra limitata viene rappresentata in due casi: quando la sezione è sull'asse reale e quando è sul semiperiodo ( al centro del rettangolo blu e su un lato), se pensiamo che il dominio dei una funzione doppiamente periodica è un toro possiamo pensare che questa rappresentazione sia dovuta a una sezione centrale di un toro, (formata da due circonferenze una limitata e una illimitata).