PENDOLI
di Massimo Fantin
gennaio 2001
Scopo
: Confronto del comportamento di diversi pendoli: cicloideo isocrono, circolare, lineare e ellittico, cicloideo bachistocrono
Uso del programma di simulazione
:
Non è necessario pensare al pendolo come ad un oggetto pesante appeso ad un filo, per avere un moto oscillatorio. Lo stesso moto lo si può realizzare obbligando una pallina a oscillare su di una guida semicilindrica o semisferica. In maniera analoga è possibile costruire un pendolo per ogni funzione matematica. Ho voluto mettere a confronto cinque tipi di pendoli che hanno degli aspetti interessanti singolarmente ed anche mettendoli a confronto.
Il pendolo cicloideo isocrono che, come è noto è il vero pendolo isocrono a differenza del pendolo sferico per il quale il periodo di oscillazione aumenta, seppur di poco all'aumentare dell'ampiezza.
Metodo numerico usato per il calcolo della posizione del pendolo cicloideo
Le equazioni parametriche della cicloide con vertice nell'origine sono
x = R(k + sin k) ; y = R (1-cos k) data l'impossibilità della risoluzione della prima equazione rispetto al parametro k e pertanto della impossibilità della esplicitazione dell'equazione rispetto a y, per poter tracciare il grafico è occorre partire dal valore della y, risolvere la seconda equazione rispetto al parametro k e dalla prima trovare i due valori di x. Per determinare la cicloide isocrona passante per un punto (x0, y0) è necessario determinare il valore di R, ma per fare questo si determina k dall'equazione x0/y0=(k+sin k)/(1-cosk), equazioni in k che viene risolta col metodo iterativo di Newton, determinato k corrispondente al punto assegnato si calcola R da una delle due equazioni date, e successivamente , procedendo come illustrato precedentemente da un valore di y si possono trovare i valori di x.
Per determinare la velocità e la posizione del pendolo si osserva che il livello di partenza corrisponde all'energia totale del sistema pertanto, dal principio di conservazione dell'energia, in ogni punto la somma delle energie potenziale e cinetica è sempre uguale a quella potenziale del livello di partenza. mgy + 1/2mv2 = mgy0 dove y0 rappresenta il livello di partenza e y il livello al quale si trova il pendolo, v il modulo della velocità, si elimina m e si risolve in v. A questo punto occorre distribuire la velocità nelle due direzioni vx e vy per far questo bisogna considerare la derivata della curva che viene calcolata per via numerica e si avrà vx = v y' / (1+ y'2) e vy = v / (1+ y'2), quest'ultima viene utilizzata per calcolare la successiva posizione del pendolo con un metodo numerico tipo Eulero.
Dimostrazione dell'isocronismo del pendolo cicloideo
Prime proprietà della cicloide.
La cicloide è la traiettoria di un punto su una circonferenza che rotola, senza strisciare, su una retta.
Per comodità prendiamo la retta orizzontale, la circonferenza sotto la retta e il punto P inizialmente in posizione opposta alla retta.
Dopo aver rotolato di un angolo 2
j la circonferenza , sia A come punto di contatto con la retta a distanza 2j R dall'origine, mentre il punto P si sarà spostato rispetto alla perpendicolare alla retta di un angolo j ( j è l'angolo alla circonferenza mentre l'angolo di rotazione è al centro ) . La tangente alla cicloide nel punto P sarà inclinata rispetto all'orizzontale dello stesso angolo j infatti la rotazione del punto P avviene intorno al punto A di contatto pertanto la tangente sarà perpendicolare alla corda AP, e naturalmente passerà per B perchè ABC è iscritto in una semicfr. Conduciamo da P la perpendicolare PH al diametro AB =2RDetto AH=y, avremo per il primo teorema di Euclide AP2= y 2R e infine
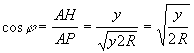
Calcoliamo ora l'elemento infinitesimo di lunghezza della curva dl
![]()
da cui, risolvendo in sinj , e con la precedente si ha:
![]()
Risolvendo rispetto a dl si ha
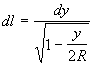
Inoltre la velocità di discesa, nella direzione del moto, per le note formule di cinematica vale
![]()
pertanto l'intervallo di tempo dt sarà:
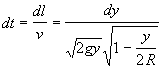
e integrando dt con y da y1 a 2R si trova il tempo di discesa,
moltiplicando per 4 si ha il periodo che risulta:
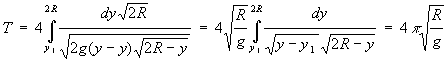
Infatti l'ultimo integrale è del tipo:
![]()
che integra facilmente con la sostituzione:
![]()
L'isocronismo si deduce dal fatto che il periodo non dipende dal livello di partenza ma solo dal raggio.
Il pendolo circolare o sferico è il pendolo considerato solitamente perché facilmente realizzabile con un peso e un filo attaccato ad un chiodo. Lo studio di questo pendolo dal punto di vista matematico è particolarmente interessante anche se presenta alcune difficoltà.
Indichiamo con
R = il raggio del cerchio entro al quale è obbligato a muoversi il peso,
y0 = il livello di partenza
j
= l'angolo tra la verticale e la posizione del pendoloy = R cos j l'altezza del pendolo rispetto al diametro orizzontale
dl =R dj = l'elemento infinitesimo di traiettoria.
Si avrà pertanto:
dj = - R sen j
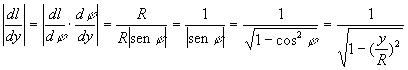
L'elemento infinitesimo temporale sarà
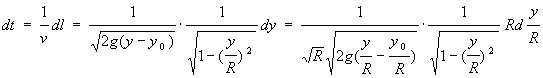
Ponendo w = y/R e w0 = y0/R si ha:
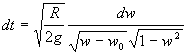
Il periodo T del pendolo cioè il tempo che impiega a compiere un'oscillazione completa sarà quattro volte il tempo impiegato per scendere dalla posizione di partenza y0 al vertice inferiore. Per calcolare il tempo di discesa si integra dt tra i suoi estremi e si moltiplica per quattro.
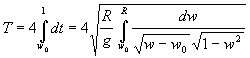
Con un ulteriore cambiamento di variabili w = w0 +(1-w0) z si ottiene, dopo aver semplificato:
|
|
(1)
Osserviamo che w0 = cos j 0 e naturalmente -1<w0<1
Studiamo ora i casi particolari:
![]() che è la nota formula.
che è la nota formula.
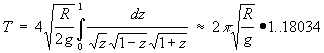
Tale integrale è calcolabile solo per via numerica. Il periodo di oscillazione di un pendolo semicircolare è circa il 18% più lungo del periodo delle piccole oscillazione dello stesso pendolo.
![]()
il che significa che il pendolo circolare è asintotico nel senso che il tempo impiegato per raggiungere la posizione di maggiore altezza è infinito.
|
w0 = cos j 0 |
T / T0 |
|
1 |
1 |
|
0.999 |
1.00013 |
|
0.99 |
1.00125 |
|
0.9 |
1.02586 |
|
0.8 |
1.02651 |
|
0.7 |
1.04104 |
|
0.6 |
1.05655 |
|
0.5 |
1.07318 |
|
0.4 |
1.09110 |
|
0.3 |
1.11049 |
|
0.2 |
1.13160 |
|
0.1 |
1.15475 |
|
0.0 |
1.18034 |
|
-0.1 |
1.20889 |
|
-0.2 |
1.24113 |
|
-0.3 |
1.27808 |
|
-0.4 |
1.32122 |
|
-0.5 |
1.37288 |
|
-0.6 |
1.43698 |
|
-0.7 |
1.52090 |
|
-0.8 |
1.64126 |
|
-0.9 |
1.85150 |
|
-0.99 |
2.57147 |
|
-0.999 |
3.30232 |
|
-0.9999 |
4.03496 |
|
-1 |
¥ |
Per uno studio più dettagliato del periodo di oscillazione al variare dell'ampiezza massima o dell'altezza del punto di partenza si integra per via numerica la (1) ottenendo la tabella a fianco nella quale si mettono a confronto i coseni delle semiampiezze massime con il rapporto tra il periodo T e il periodo del pendolo di piccola apertura T0:
Nel grafico a fianco è rappresentato l'andamento del rapporto T/T0 al variare di cosj .
Nella parte inferiore è rappresentata la semicirconferenza goniometrica che consente di determinare graficamente il rapporto T/T0 direttamente dalla semiampiezza rappresentata inferiormente, si osserva che se l'ampiezza è inferiore a pochi gradi non si ha una sensibile variazione del periodo..
Il pendolo lineare nel quale il percorso della pallina è una doppia rampa (l'equazione cartesiana è y = m |x| con m>0 e che può essere studiato matematicamente in modo elementare e per il quale è anche facile trovare la relazione esistente tra l'altezza del punto di partenza ed il periodo di oscillazione.
Sia y0 il livello di partenza, il pendolo si muove sul piano inclinato con pendenza m ed è soggetto all'accelerazione di gravità: g, la componente dell'accelerazione nella direzione del piano inclinato vale:
![]()
analogamente, la lunghezza del piano inclinato è:
![]()
sostituendo questi valori nell'equazione della cinematica
l = 1/2 a t2 e risolvendo in t si trova il tempo di discesa,
il periodo di oscillazione T è quattro volte tanto ovvero:
|
|
Come si vede dalla formula il periodo di oscillazione è proporzionale alla radice quadrata del rapporto tra l'altezza di caduta e l'accelerazione di gravità. Non si tratta pertanto di un pendolo tendenzialmente isocrono come invece è quello circolare.
Il pendolo Ellittico ha per traiettoria una semiellisse con vertice nell'origine e avente per semiassi le coordinate del punto di partenza (x0,y0)
Il pendolo cicloideo bachistocrono il cui periodo di oscillazione è il più piccolo possibile, per rendersene conto è sufficiente far scendere le palline contemporaneamente dal punto più alto e osservare che la pallina che si muove su un percorso cicloideo bachistocrono raggiunge per prima il punto più basso.
Dal punto di vista matematico, per dimostrare che il pendolo cicloideo con partenza dalla cuspide costituisce il percorso più veloce si deve ottimizzare il tempo.
Sapendo che la velocità è proporzionale alla radice quadrata di y si dovrà ottimizzare l'integrale:
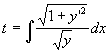
Per questo si applica l'equazione di Eulero che consente di ottimizzare i funzionali ![]()
Mediante l'equazione F-y' F'y' = c con c costante.
Nel nostro caso l'equazione di Eulero diventa:
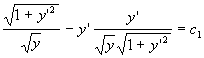
e semplificando si ha:
![]()
Risolvendo rispetto ad y' si ha:

dove a è il complementare dell'angolo tra la tangente alla curva e l'asse x (vedi figura del pendolo cicloideo).
Queste osservazioni sono sufficienti per dire che il pendolo più veloce (bachistocrono) è il pendolo cicloideo. La differenza tra il pendolo isocrono e quello bachistocrono è che il primo è simmetrico rispetto al vertice mentre il secondo inizia nella cuspide con tangente verticale.
Per realizzare numericamente questo secondo pendolo si è proceduto in modo analogo al caso del pendolo isocrono: con la differenza che in questo caso il parametro R del pendolo doveva essere determinato conoscendo la posizione di partenza x0, y0 (la cuspide) e un punto, l'origine delle coordinate, si determina il vertice della cicloide traslata x0-p R, y0-2R e procedendo come nell'altro caso si trova il valore di k corrispondente al punto noto e R, con esso, dalle equazioni della cicloide traslata si costruisce una semicurva e simmetricamente l'altra metà.
Nel caso in cui il punto di partenza si trovi in posizione irraggiungibile: x0 > 2/p y0 la bachistocrona che porta all'origine è costituita dal raccordo della cicloide con cuspide nel punto x0, y0 e con vertice sull'asse delle x e dal segmento di asse x.
Uso del programma di simulazione
L'uso del programma di simulazione è molto semplice:
ciascun pendolo è caratterizzato da un colore e da un pulsante, quando il pendolo è attivo il pulsante assume il colore del pendolo altrimenti è grigio chiaro.
Il livello di partenza del/i pendolo/i è segnato da una linea azzurra orizzontale che può essere spostata con il mouse.
Si possono attivare più pendoli contemporaneamente, in tal caso per poter confrontare i risultati è necessario portare il livello di partenza al massimo in modo che le palline partano dallo stesso punto.
Il tasto via fa partire i pendoli e il cronometro mentre per fermare il cronometro di usa il tasto stop, attenzione che lo stop avviene non quando si preme il pulsante stop ma quando lo si lascia.
E' possibile allargare, restringere i pendoli trascinando l'estremo alto a sinistra (pallino giallo) con il mouse,
Verifica della legge di isocronismo del pendolo cicloideo
Si attiva il solo pendolo cicloideo (Colore verde) e si posiziona l'estremo superiore nella zona inferiore alla linea gialla ( questo perché se il punto di partenza è al di sopra di detta linea non è possibile realizzare un pendolo totalmente isocrono, sarà isocrona solo la parte inferiore curva).
Posizionare la linea azzurra corrispondente al livello di partenza ad una certa altezza, fare partire il pendolo e fermarlo quando ha compiuto una oscillazione completa ( fare attenzione che il tasto stop ferma il moto quando lo si lascia e non quando lo si preme) annotare il tempo impiegato. Ripetere la prova per altre altezze senza modificare la forma del pendolo.
Scrivere una tabella e verificare che il tempo non è cambiato nell'ambito degli errori di misura.
Posizione dell'estremo sinistro: x0 = _______________ y0=5
|
Altezza (metri) |
Periodo (secondi) |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
Verificare infine che il valore del periodo trovato sperimentalmente è compatibile con quello trovato per via teorica
Determinazione della legge esatta del pendolo circolare.
Procedere in modo analogo al caso precedente utilizzando questa volta un pendolo circolare (colore rosso) fissando una volta per tutte il raggio di curvatura e annotando alle diverse altezze i corrispondenti tempi: questa volta è bene effettuare diverse prove per poter meglio determinare la legge che si tratterà di una legge non lineare e pertanto potremo approssimarla con una funzione polinomiale.
Raggio 10 metri
|
Altezza di partenza (metri) |
Periodo (secondi) |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
Quando si è riempita la tabella, per determinare la legge matematica che lega l'altezza di partenza con il periodo si può utilizzare il programma di interpolazione polinomiale presente in questo sito e cercare la curva interpolante che meglio approssima tutti i punti trovati
Rappresentare in un grafico cartesiano il grafico della legge determinata, i punti trovati in corrispondenza della misure fatte e verificare se i valori trovati sperimentalmente concordano con quelli teorici
Determinazione della legge del pendolo lineare
Si procede in modo analogo ai precedenti osservando però che questa volta la legge non assomiglia ad una di isocronismo nel senso che anche per piccole aperture i tempi di oscillazione aumentano all'aumentare dell'altezza e la legge che si viene a trovare è una legge di tipo quadratico. E' compito dello studente determinare sperimentalmente l'espressione analitica della legge e verificare che coincide, nei limiti degli errori di misura con quella determinata par via teorica.
Altezza 10 metri
|
h altezza di partenza (m) |
T periodo (sec) |
T2 / h |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|